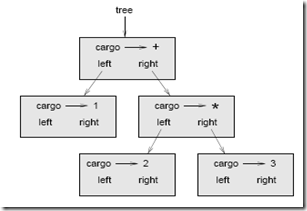
En esta sección analizamos expresiones infijas y formamos los correspondientes arboles de expresión. Por ejemplo, la expresión (3+7)*9 nos da el siguiente árbol:
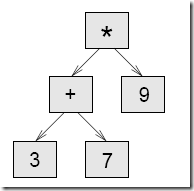
Fíjese en que hemos simplificando el diagrama omitiendo los nombres de los atributos.
El analizador que vamos a escribir maneja expresiones que incluyen números, paréntesis y los operadores + y *.
Suponemos que la cadena de entrada ya ha sido tokenizada y almacenada en una lista de Python. La lista de tokens d (3+7)*9 es:
[‘(‘, 3, ‘+’, 7, ‘)’, ‘*’, 9, ‘fin’]
El token fin es útil para evitar que el analizador lea mas allá del final de la lista.
A modo de ejercicio, escriba una función que tome una cadena conteniendo una expresión y devuelva una lista de tokens.
La primera función que vamos a escribir es tomaToken, que toma como parámetros una lista de tokens y el token que esperamos. Compara el token esperado con el primer token de la lista: si coinciden, elimina el token de la lista y devuelve
verdadero, en caso contrario, devuelve falso:
1: def tomaToken(listaToken, esperado):
2: if listaToken[0] == esperado:
3: del listaToken[0]
4: return 1
5: else:
6: return 0
Como listaToken apunta a un objeto mutable, los cambios hechos aquí son visibles para cualquier otra variable que apunte al mismo objeto.
La siguiente función, obtieneNumero, maneja operandos. Si el siguiente token de listaToken es un numero, obtieneNumero lo elimina y devuelve un nodo hoja que contiene el numero; en caso contrario, devuelve None.
1: def obtieneNumero(listaToken):
2: x = listaToken[0]
3: if type(x) != type(0): return None
4: del listaToken[0]
5: return Arbol (x, None, None)
Antes de seguir, debemos probar obtieneNumero aisladamente. Asignamos una lista de números a listaToken, extraemos el primero, imprimimos el resultado e imprimimos lo que quede de la lista de tokens:
1: >>> listaToken = [9, 11, 'fin']
2: >>> x = obtieneNumero(listaToken)
3: >>> imprimeArbolPostfijo(x)
4: 9
5: >>> print listaToken
6: [11, 'fin']
El siguiente metodo que necesitamos es obtieneProducto, que construye un árbol de expresión para productos. Un producto simple tiene dos números como
operandos, como 3 * 7.
Aquí tenemos una versión de obtieneProducto que maneja productos simples.
1: def obtieneProducto(listaToken):
2: a = obtieneNumero(listaToken)
3: if tomaToken(listaToken, '*'):
4: b = obtieneNumero(listaToken)
5: return Arbol ('*', a, b)
6: else:
7: return a
Suponiendo que obtieneNumero se ejecuta con éxito y devuelve un árbol simple, asignamos el primer operando a a. Si el siguiente carácter es *, obtenemos el segundo numero y construimos un árbol de expresión con a, b, y el operador.
Si el siguiente carácter es cualquier otra cosa, simplemente devolvemos el nodo hoja con a. Veamos dos ejemplos:
1: >>> listaToken = [9, '*', 11, 'fin']
2: >>> arbol = obtieneProducto(listaToken)
3: >>> imprimeArbolPostfijo(arbol)
4: 9 11 *
5: >>> listaToken = [9, '+', 11, 'fin']
6: >>> arbol = obtieneProducto(listaToken)
7: >>> imprimeArbolPostfijo(arbol)
8: 9
El segundo ejemplo implica que entendemos un operando suelto como un tipo de producto. Esta definición de producto” es contraria a la intuición, pero resulta ser útil.
Ahora tenemos que vernos las con productos compuestos, como 3 * 5 * 13.
Tratamos esta expresión como un producto de productos, es decir, 3 * (5 *13). El árbol resultante es:
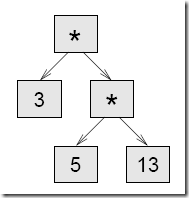
Con un pequeño cambio en obtieneProducto podemos manejar productos arbitrariamente largos:
1: def obtieneProducto(listaToken):
2: a = obtieneNumero(listaToken)
3: if tomaToken(listaToken, '*'):
4: b = obtieneProducto(listaToken) # cambiamos esta l¶³nea
5: return Arbol ('*', a, b)
6: else:
7: return a
En otras palabras, un producto puede ser bien un operando aislado o un árbol con * en su raíz, un numero en la derecha y un producto en la izquierda. Este tipo de definición recursiva deber³a empezar a resultar familiar.
Comprobemos la nueva versión con un producto compuesto:
1: >>> listaToken = [2, '*', 3, '*', 5 , '*', 7, 'fin']
2: >>> arbol = obtieneProducto(listaToken)
3: >>> imprimeArbolPostfijo(arbol)
4: 2 3 5 7 * * *
Ahora añadiremos la capacidad de analizar sumas. De nuevo, usamos una definición poco intuitiva de suma”. Para nosotros, una suma puede ser un árbol con + en la ra³z, un producto en la izquierda y una suma en la derecha. O también, una suma puede ser simplemente un producto.
Si quiere seguir adelante con esta definición, tiene una bonita propiedad: podemos representar cualquier expresión (sin paréntesis) como una suma de productos. Esta propiedad es la base de nuestro algoritmo de analisis.
obtieneSuma intenta construir un árbol con un producto en la izquierda y una suma en la derecha. Pero si no encuentra un +, simplemente construye un producto.
1: def obtieneSuma(listaToken):
2: a = obtieneProducto(listaToken)
3: if tomaToken(listaToken, '+'):
4: b = obtieneSuma(listaToken)
5: return Arbol ('+', a, b)
6: else:
7: return a
Vamos a probarla con 9 * 11 + 5 * 7:
1: >>> listaToken = [9, '*', 11, '+', 5, '*', 7, 'fin']
2: >>> arbol = obtieneSuma(listaToken)
3: >>> imprimeArbolPostfijo(arbol)
4: 9 11 * 5 7 * +
Ya casi hemos acabado, pero todavía tenemos que manejar los paréntesis.
En cualquier lugar de una expresión donde puede haber un numero, puede haber también una suma entera entre paréntesis. Solo necesitamos modificar
obtieneNumero para manejar subexpresiones:
1: def obtieneNumero(listaToken):
2: if tomaToken(listaToken, '('):
3: x = obtieneSuma(listaToken) # obtiene la subexpresi¶on
4: tomaToken(listaToken, ')') # quita el cierre de par¶entesis
5: return x
6: else:
7: x = listaToken[0]
8: if type(x) != type(0): return None
9: listaToken[0:1] = []
10: return Arbol (x, None, None)
Vamos a probar este código con 9 * (11 + 5) * 7:
1: >>> listaToken = [9, '*', '(', 11, '+', 5, ')', '*', 7, 'fin']
2: >>> arbol = obtieneSuma(listaToken)
3: >>> imprimeArbolPostfijo(arbol)
4: 9 11 5 + 7 * *
El analizador manejo correctamente los paréntesis; la suma ocurre antes de la multiplicación.
En la versión final del programa, sería bueno dar a obtieneNumero un nombre mas descriptivo de su nueva función.