Cesar Systems

Este capítulo presenta dos TADs: la Cola y la Cola Priorizada. En la vida real, una cola es una fila de clientes esperando un servicio de algún tipo. En la mayoría de los casos, el primer cliente de la fila es el primero al que se va a servir. Sin embargo, hay excepciones. En los aeropuertos, a veces se saca de la cola a los clientes cuyos vuelos van a salir pronto. En los supermercados, un cliente educado puede dejar que alguien que lleva pocos productos pase antes.

La regla que determina quien va primero se llama táctica de encolamiento. La táctica de encolamiento mas simple se llama FIFO, de “first-in-firrst-out”, el primero que entra es el primero que sale”. La táctica de encolamiento mas general es el encolamiento priorizado, en la que a cada cliente se le asigna una prioridad y el cliente con la prioridad mas alta pasa primero, sin importar el orden de llegada. Decimos que es la tactica mas general porque la prioridad se puede basar en cualquier cosa: a que hora sale el vuelo; cuantos productos lleva el cliente; cuan importante es el cliente. Por supuesto, no todas las tácticas de prioridad son justas”, pero la justicia siempre es subjetiva.

El TAD Cola y el TAD Cola Priorizada tienen el mismo conjunto de operaciones.

La diferencia esta en la semántica de las operaciones: una cola usa la táctica FIFO, y una cola priorizada (como su propio nombre indica) usa una táctica de encolamiento priorizado.

19.1. El TAD Cola

El TAD Cola se define a través de las siguientes operaciones:

__init__ : Inicializa una cola nueva vacía.

inserta: Añade un elemento a la cola.

quita: Elimina y devuelve un elemento de la cola. El elemento devuelto es el primero que se añadió.

estaVacia: Comprueba si la cola esta vacía.

19.2. Cola Enlazada

La primera implementación del TAD Cola al que vamos a echar un vistazo se llama cola enlazada porque esta hecha de objetos Nodo enlazados. He aquí

la definición de la clase:

class Cola:
    def __init__(self):
        self.longitud = 0
        self.cabeza = None
    def estaVacia(self):
        return (self.longitud == 0)
    def inserta(self, carga):
        nodo = Nodo(carga)
        nodo.siguiente = None
        if self.cabeza == None:
            # si la lista esta vac³a el nuevo nodo va el primero
            self.cabeza = nodo
        else:
            # encuentra el ultimo nodo de la lista
            ultimo = self.cabeza
        
        while ultimo.siguiente: ultimo = ultimo.siguiente
            # añadir el nuevo nodo
            ultimo.siguiente = nodo
            self.longitud = self.longitud + 1
    def quita(self):
        carga = self.cabeza.carga
        self.cabeza = self.cabeza.siguiente
        self.longitud = self.longitud - 1
        return carga

Los métodos estaVacia y quita son idénticos a los métodos estaVacia y a quitaPrimero de ListaEnlazada. El metodo inserta es nuevo y un poco mas complicado.

Queremos insertar nuevos elementos al final de la lista. Si la cola esta vacía, simplemente hacemos que cabeza se refiera al nuevo nodo.

En caso contrario, recorremos la lista hasta el ultimo nodo y lo fijamos al final.

Podemos reconocer el ultimo nodo porque su atributo siguiente es None.

En un objeto Cola correctamente construido hay dos invariantes. El valor de longitud debería ser el numero de nodos en la cola, y el ultimo nodo debería tener siguiente igual a None. Crease que este metodo cumple con ambas invariantes.

19.3. Rendimiento típico

Normalmente cuando invocamos un metodo, no nos importan los detalles de su implementación. Pero hay un “detalle” que podría interesarnos: el rendimiento típico del metodo.

¿Cuanto tarda, y como var³a el tiempo de ejecución al aumentar el numero de elementos de la colección?

Primero mire quita. Ahí no hay bucles ni llamadas a funciones, dando a entender que el tiempo de ejecución de este metodo es siempre el mismo. Un metodo así se llama operación de tiempo constante. En realidad, el metodo podría
ser ligeramente mas rápido cuando la lista esta vacía porque se salta el cuerpo de la condición, pero esa diferencia no es significativa.

El rendimiento de inserta es muy diferente. En el caso general, tenemos que recorrer la lista para encontrar el ultimo elemento.

Este recorrido cuesta un tiempo proporcional a la longitud de la lista. Como el tiempo de ejecución es función lineal de la longitud, este metodo se llama de tiempo lineal. Comparado con el tiempo constante, es muy pobre.

19.4. Cola Enlazada Mejorada

Nos gustaría una implementación del TAD Cola capaz de realizar todas las
operaciones en tiempo constante. Una forma de hacerlo es modificar la clase
Cola de modo que mantenga una referencia tanto al primero como al ultimo
nodo, como se muestra en la figura:

La implementación de ColaMejorada es así:

class ColaMejorada:
    def __init__(self):
        self.longitud = 0
        self.cabeza = None
        self.ultimo = None
    def estaVacia(self):
        return (self.longitud == 0)

Hasta ahora, el único cambio es el atributo ultimo. Se usa en los métodos
inserta y quita:

class ColaMejorada:
...
def inserta(self, carga):
    nodo = Nodo(carga)
    nodo.siguiente = None
    if self.longitud == 0:
        # si la lista esta vac³a, el nuevo nodo es cabeza y ultimo
        self.cabeza = self.ultimo = nodo
    else:
        # encontrar el ultimo nodo
        ultimo = self.ultimo
        # añaadir el nuevo nodo
        ultimo.siguiente = nodo
        self.ultimo = nodo
    self.longitud = self.longitud + 1

Como ultimo sigue el rastro del ultimo nodo, no necesitamos buscarlo. A causa
de esto, este metodo funciona en tiempo constante.

Debemos pagar un precio por esa velocidad. Tenemos que añadir un caso especial
a quita para apuntar ultimo a None cuando quitamos el ultimo nodo:

class ColaMejorada:
...
    def quita(self):
        carga = self.cabeza.carga
        self.cabeza = self.cabeza.siguiente
        self.longitud = self.longitud - 1
        if self.longitud == 0:
        self.ultimo = None
    return carga

Esta implementación es mas complicada que la de la Lista Enlazada, y es mas
difícil demostrar que es correcta. La ventaja es que hemos alcanzado la meta:
tanto inserta como quita son operaciones de tiempo constante.

Como ejercicio, escriba una implementación del TAD Cola usando
una lista de Python. Compare el rendimiento de esta implementación
con la de la ColaMejorada para varias longitudes de cola.

19.5. Cola priorizada

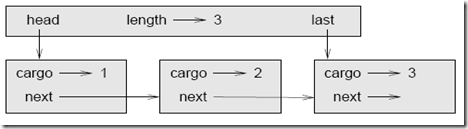
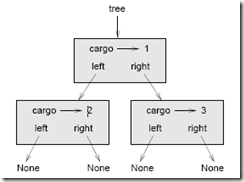
El TAD Cola Priorizada tiene el mismo interfaz que el TAD Cola, pero diferente semántica. De nuevo, el interfaz es:
__init __: Inicializa una cola vacía nueva.

inserta: Añade un nuevo elemento a la cola.

quita: Elimina y devuelve un elemento de la cola. El elemento devuelto es el de prioridad mas alta.

estaVacia: Comprueba si la cola esta vacía.

La diferencia semántica es que el elemento eliminado de la cola no es necesariamente el primero que se añadió. En su lugar, es el elemento con la prioridad mas alta. Lo que son las prioridades y como se comparan con las otras no se especifica en la implementación de la Cola Priorizada. Depende de los elementos de la cola.

Por ejemplo, si los elementos de la cola tienen nombres, podemos elegirlos en orden alfabético. Si son puntuaciones de bolos, podemos ir de mayor a menor, pero si son puntuaciones de golf, iremos de menor a mayor. Siempre que podamos
comparar los elementos de la cola, podremos encontrar y quitar el elemento con mayor prioridad.

Esta implementación de Cola Priorizada tiene como atributo una lista de Python que contiene los elementos de la cola.

class ColaPriorizada:
    def __init__(self):
        self.elementos = []
    def estaVacia(self):
        return self.elementos == []
    def inserta(self, elemento):
        self.elementos.append(elemento)

El metodo de inicializacion, estaVacia, e inserta son todos calcados de las operaciones sobre listas. El único metodo interesante es quita:

class ColaPriorizada:
...
    def quita(self):
        maxi = 0
        for i in range(1,len(self.elementos)):
        if self.elementos[i] > self.elementos[maxi]:
        maxi = i
        elemento = self.elementos[maxi]
        self.elementos[maxi:maxi+1] = []
        return elemento

Al principio de cada iteración, maxi contiene el índice del elemento mas grande
(prioridad mas alta) que hemos visto hasta el momento. Cada vez que se com-
pleta el bucle, el programa compara el iésimo elemento con el campeón. Si el
nuevo elemento es mayor, el valor de maxi se fija a i.
Cuando la sentencia for completa su ejecución, maxi es el índice del elemento
mayor. Este elemento se elimina de la lista y se devuelve.

Vamos a probar la implementación:

>>> c = ColaPriorizada()
>>> c.inserta(11)
>>> c.inserta(12)
>>> c.inserta(14)
>>> c.inserta(13)
>>> while not c.estaVacia(): print c.quita() # ver cu¶al se quita
14
13
12
11

Si la cola contiene números o cadenas simples, se eliminan en orden numérico o alfabético, de mayor a menor. Python puede encontrar el entero o la cadena mayor porque puede compararlos usando los operadores de comparación internos.

Si la cola contiene un tipo de objeto, debe proporcionar un metodo __cmp__ . Cuando quita usa el operador > para comparar elementos, invoca al __cmp__ de uno de los elementos y le pasa el otro como parámetro. Siempre que el metodo __cmp__ trabaje adecuadamente, la Cola Priorizada funcionara.

19.6. La clase Golfista

Como ejemplo de un objeto con una definición inusual de prioridad, vamos a
implementar una clase llamada Golfista que mantiene los nombres y puntua-
ciones de golfistas. Como es habitual, empezamos por definir __init__ y __str__:

class Golfista:
    def __init__(self, nombre, puntos):
        self.nombre = nombre
        self.puntos = puntos
    def __str__(self):
        return "%-16s: %d" % (self.nombre, self.puntos)

__str__ usa el operador de formato para poner los nombres y las puntuaciones
en bonitas columnas.
A continuación definimos una versión de __cmp__ en la que la puntuación mas
baja tiene la prioridad mas alta. Como siempre, __cmp__ devuelve 1 si self es
mayor que” otro, -1 si self es menor que” otro, y 0 si son iguales.

class Golfista:
...
    def __cmp__(self, otro):
        if self.puntos < otro.puntos: return 1 # menos es mas
if      self.puntos > otro.puntos: return -1
        return 0

Ya estamos listos para probar la cola priorizada con la clase Golfista:

>>> tiger = Golfista("Tiger Woods", 61)
>>> cabr = Golfista("Angel Cabrera", 72)
>>> ola = Golfista("J.M. Olazabal", 69)
>>> cp = ColaPriorizada()
>>> cp.inserta(tiger)
>>> cp.inserta(cabr)
>>> cp.inserta(ola)
>>> while not cp.estaVacia(): print cp.quita()
Tiger Woods : 61
J.M. Olazabal : 69
Angel Cabrera : 72

Como ejercicio, escriba una implementación del TAD Cola Prio-
rizada usando una lista enlazada. Deber³a usted mantener la lista
ordenada de modo que la eliminación sea una operación de tiempo
constante. Compare el rendimiento de esta implementación con la
implementación con la lista de Python.

19.7. Glosario

cola: Un conjunto ordenado de objetos esperando un servicio de algún tipo.

Cola: Un TAD que ejecuta las operaciones que uno podría realizar sobre una cola.

Táctica de encolamiento: Las reglas que determinan que miembro de la cola será el próximo en eliminarse.

FIFO: “First In, First Out”, una táctica de encolamiento en la que el primer miembro en llegar es el primero en salir.

cola priorizada: Una táctica de encolamiento en la que cada miembro tiene una prioridad determinada por factores externos. El miembro con mayor prioridad es el primero en eliminarse.

Cola Priorizada: Un TAD que define las operaciones que se pueden realizar sobre una cola priorizada.

cola enlazada: Una implementación de una cola utilizando una lista enlazada.

tiempo constante: Una operación cuyo tiempo de ejecución no depende del tamaño de la estructura de datos.

tiempo lineal: Una operación cuyo tiempo de ejecución es función lineal del tamaño de la estructura de datos.

Árboles

Al igual que las listas enlazadas, los arboles están hechos de nodos. Un tipo
común de árbol es un árbol binario, en el que cada nodo contiene una referencia
a otros dos nodos (posiblemente nula). Nombramos a estas referencias como
subarboles izquierdo y derecho. Como los nodos de las listas, los nodos de los
arboles también contienen una carga. Un diagrama de estado de un árbol es así:

Para evitar apelotonar las cosas en la figura, solemos omitir los Nones.

La parte superior del árbol (el nodo al que apunta tree) se llama raíz. Siguiendo con la metáfora del árbol, los otros nodos se llaman ramas y los nodos de los extremos con referencias nulas se llaman hojas. Puede parecer extraño que
dibujemos la figura con la raíz arriba y las hojas abajo, pero eso no es lo mas raro.

Para empeorar las cosas, los científicos informáticos añaden a la mezcla otra metáfora: el árbol genealógico. El nodo superior se llama a veces padre y los nodos a los que se refiere son sus hijos. Los nodos con el mismo padre se llaman hermanos.

Para terminar, tenemos un vocabulario geométrico para hablar sobre los arboles.

Ya hemos mencionado izquierda y derecha, pero también están arriba” (hacia el padre/raíz) y abajo” (hacia los hijos/hojas). También, todos los nodos que están a la misma distancia de la raíz forman un nivel del árbol.

Probablemente no sean necesarias las metáforas arbóreas para hablar de arboles, pero ahí están.

Igual que las listas enlazadas, los arboles son estructuras de datos recursivas

porque se definen recursivamente.
Un árbol es:

el árbol vacío, representado por None, o
un nodo que contiene una referencia a un objeto y dos referencias a arboles.

20.1. Crear árboles