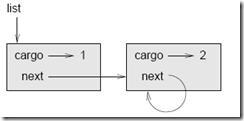
Las listas son útiles porque aportan un modo de ensamblar múltiples objetos dentro de una única entidad, a veces llamada colección. En el ejemplo, el primer nodo de la lista sirve como referencia a la lista completa.
Para pasar la lista como parámetro, solo tenemos que hacer referencia al primer nodo. Por ejemplo, la función imprimeLista toma como argumento un nodo simple. Empezando con la cabeza de la lista, imprime cada nodo hasta que llega al final.
1: def imprimeLista(nodo):
2: while nodo:
3: print nodo,
4: nodo = nodo.siguiente
5: print
1: >>> imprimeLista(nodo1)
2: 1 2 3
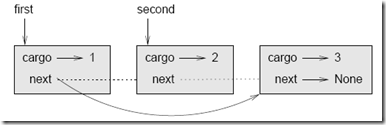
Dentro de imprimeLista tenemos una referencia al primer nodo de la lista, pero no hay una variable que haga referencia a los otros nodos. Tendremos que usar el valor de siguiente de cada nodo para acceder al siguiente nodo.
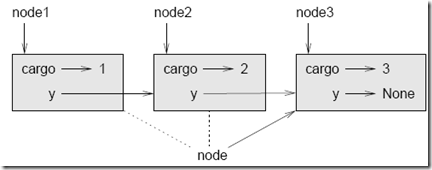
Para recorrer una lista enlazada es habitual usar la variable de un bucle como nodo para hacer referencia sucesivamente a cada uno de los nodos.
Este diagrama muestra el valor de lista y los valores que va tomando nodo:
Por convenio, las listas suelen imprimirse entre corchetes con comas entre los elementos, como [1, 2, 3]. Como ejercicio, modifique imprimeLista para que genere una salida con este formato.