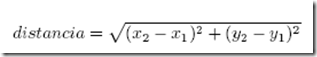Para escribir programas útiles, casi siempre necesitamos la capacidad de comprobar ciertas condiciones y cambiar el comportamiento del programa en consonancia. Las sentencias condicionales nos dan esta capacidad. La forma mas sencilla es la sentencia if:

   1: if x > 0:

   2:     print "x es positivo"

La expresion booleana tras el if se llama condicion. Si es verdadera, entonces la sentencia indentada se ejecuta. Si la condicion no es verdadera, no pasa nada.

Como otras sentencias compuestas, if consta de una cabecera y un bloque de sentencias:

   1: CABECERA:

   2: PRIMERA SENTENCIA

   3: ...

   4: ULITMA SENTENCIA

A veces hay mas de dos posibilidades y necesitamos mas de dos ramas. Una forma de expresar tal computación es un condicional encadenado:

   1: if x < y:

   2: print x, "es menor que", y

   3: elif x > y:

   4: print x, "es 

   5: mayor que", y

   6: else:

   7: print x, "y", y, "son iguales"

elif es una abreviatura de “else if“. De nuevo, solo se ejecutara una rama. No hay límite al numero de sentencias elif, pero solo se permite una sentencia

   1: else (que puede omitirse) y debe ser la ultima rama de la sentencia:

   2:     if 

   3:         eleccion == 'A':

   4:         funcionA()

   5:     elif eleccion == 'B':

   6:         funcionB()

   7:     elif 

   8:         eleccion == 'C':

   9:         funcionC()

  10:     else:

  11:         print "Eleccion no valida."

  12:     

Las condiciones se comprueban en orden. Si la primera es falsa, se comprueba la siguiente, y así. Si una de ellas es cierta, se ejecuta la rama correspondiente y termina la sentencia. Incluso si es cierta mas de una condicion, solo se ejecuta la primera rama verdadera.

Como ejercicio, envuelva estos ejemplos en funciones llamadas compara(x, y) y resuelve(eleccion).

Una condición puede estar anidada dentro de otra. Podíamos haber escrito así el ejemplo de tricotomía:

   1: if x == y:

   2:     print x, "y", y, "son iguales"

   3: else:

   4:     if x < y:

   5:         print 

   6:         x, "es menor que", y

   7:     else:

   8:         print x, "es mayor que", y

La condicion externa que contiene dos ramas. La primera rama contiene una sentencia simple de salida. La segunda rama contiene otra sentencia if, que tiene dos ramas en sí misma. Estas dos ramas son ambas sentencias de salida de datos, aunque podrían ser igualmente sentencias condicionales.

Aunque la indentacion de las sentencias hace la estructura evidente, las condiciones anidadas en seguida se vuelven difíciles de leer. En general es una buena idea evitarlas cuando pueda.

Los operadores logicos suelen facilitar un modo de simplificar las sentencias condicionales anidadas. Por ejemplo, podemos reescribir el codigo siguiente con un solo condicional:

   1: if 0 < x:

   2:     if x < 10:

   3:         print "x es un numero positivo de un dígito."

La sentencia print solo se ejecuta si conseguimos superar ambos condicionales, así que podemos usar el operador and:

La sentencia return le permite terminar la ejecución de una función antes de alcanzar su final. Una razón para usarla es detectar una condición de error:

   1: import math

   2:     def imprimeLogaritmo(x):

   3:         if x <= 0:

   4:             print "Solo numeros positivos, por favor."

   5:             return 

   6:         result = math.log(x)

   7:         print "El log de x es", result

La funcion imprimeLogaritmo toma un parametro llamado x. Lo primero que hace es comprobar si x es menor o igual que cero, en cuyo caso muestra un mensaje de error y luego usa return para salir de la funcion. El flujo de la ejecución vuelve inmediatamente al llamante y no se ejecutan las líneas restantes de la funcion.

Recuerde que para usar una funcion del modulo math tiene que importarlo.

Ya mencionamos que es legal que una función llame a otra, y de ello hemos visto ya varios ejemplos. Olvidamos mencionar que también es legal que una función se llame a sí misma. Puede no resultar evidente por que es bueno esto, pero viene a resultar una de las cosas mas interesantes y curiosas que puede hacer un programa. Examine por ejemplo la siguiente función:

   1: def cuenta_atras(n):

   2:     if n == 0:

   3:         print "Despegando!"

   4:     else:

   5:         print  n cuenta_atras(n-1)

   6:     

cuenta atras espera que su parametro, n, sea un entero positivo. Si n el parámetro es cero, muestra la palabra “¡Despegando!”. En otro caso, muestra n y luego llama a la funcion llamada cuenta atras (ella misma) pasandole como argumento n-1.

¿Que sucede si llamamos a la funcion de la siguiente manera?

   1: >>> cuenta_atras(3)

La ejecucion de cuenta atras comienza con n=3, y puesto que n no es cero, da como salida el valor 3, y luego se llama a sí misma …

La ejecucion de cuenta atras comienza con n=2, y puesto que n no es cero, muestra el valor 2 y luego se llama a sí misma …

La ejecucion de cuenta atras comienza con n=1, y puesto que n no es cero, muestra el valor 1, y luego se llama a
sí misma…

La ejecucion de cuenta atras comienza con n=0, y puesto que n es cero, muestra la palabra Despegando!” y luego retorna.

La cuenta atras que dio n=1 retorna.

La cuenta atras que dio n=2 retorna.

La cuenta atras que dio n=3 retorna.

Y entonces ya esta de vuelta en main (menudo viaje). De manera que la salida completa presenta el siguiente aspecto:

3

2

1

¡Despegando!

Como segundo ejemplo, consideremos de nuevo las funciones nuevaLinea and tresLineas.

   1: def nuevaLinea():

   2:     print    

   3: def 

   4:     tresLineas():

   5:     nuevaLinea()

   6:     nuevaLinea()

   7:     nuevaLinea()

Aunque todas funcionan, no serían de mucha ayuda si quisiera mostrar 2 líneas nuevas o 106. Una mejor alternativa será:

   1: def nLineas(n):

   2: if n > 0:

   3: print

   4: nLineas(n-1)

Este programa es parecido a cuenta atras; mientras n sea mayor que cero, muestra una nueva l³nea, y luego se llama a sí misma para mostrar >n-1 nuevas líneas mas. De esta manera, el numero total de nuevas l³neas es 1 + (n-1), que si rescata su algebra vera que es n.

El proceso por el que una funcion se llama a s³ misma se llama recursividad, y dichas funciones se denominan recursivas.

El la Sección 3.11 utilizamos un diagrama de pila para representar el estado de un programa durante la llamada de una función. El mismo tipo de diagrama puede hacer mas fácil interpretar una función recursiva.

Cada vez que se llama a una función, Python crea un nuevo marco para la función, que contiene sus variables locales y parámetros. En el caso de una función recursiva, puede haber mas de un marco en la pila al mismo tiempo.

La figura muestra un diagrama de pila para cuenta atrás, invocada con n = 3:

Como es habitual, en lo alto de la pila esta el marco de main . Esta vac³a porque no hemos ninguna variable sobre main ni le hemos pasado ningún parámetro.

Los cuatro marcos de cuenta atrás tienen valores diferentes para el parámetro n. El fondo de la pila, donde n=0, se llama caso base. No hace una llamada recursiva, de manera que no hay mas marcos.

Como actividad, dibuje un diagrama de pila para nLineas, invocada con el parámetro n=4.

Los programas que hemos escrito hasta ahora son un poco maleducados en el sentido de que no aceptan entradas de datos del usuario.

Simplemente hacen lo mismo siempre.

Python proporciona funciones internas que obtienen entradas desde el teclado.

La mas sencilla se llama raw input. Cuando llamamos a esta función, el programa se detiene y espera a que el usuario escriba algo. Cuando el usuario pulsa la tecla Return o Entre, el programa se reanuda y raw input devuelve lo que el usuario escribió como tipo string:

   1: >>> entrada = raw_input ()

   2: ¿A que estas esperando?

   3: >>> print entrada A que estas esperando?

Antes de llamar a raw input es conveniente mostrar un mensaje que le pida al usuario el dato solicitado. Este mensaje se llama indicador (prompt en ingles).

Puede proporcionarle un indicador a raw input como argumento:

   1: >>> nombre = raw_input ("Como te llamas? ")

   2: Como te llamas? Hector, 

   3: heroe de los Troyanos!

   4: >>> print nombre

   5: Hector, heroe de los 

   6: Troyanos!

Si espera que la entrada sea un entero, utilice la función input. Por ejemplo:

   1: >>> indicador = 

   2: ... "Cual es la velocidad de una golondrina sin 

   3: carga?n"

   4: >>> velocidad = input (indicador)

Si el usuario teclea una cadena de números, se convertirá en un entero y se asignara a velocidad. Por desgracia, si el usuario escribe algo que no sea un dígito, el programa dará un error:

   1: >>> velocidad = input (indicador)

   2: Cual es la velocidad de una 

   3: golondrina sin carga?

   4: Se refiere usted a la golondrina europea o a la 

   5: africana?

   6: SyntaxError: invalid syntax

Para evitar este tipo de error, generalmente es buena idea usar raw input para obtener una cadena y usar entonces las funciones de conversión para convertir a otros tipos.

operador modulo: Operador, señalado con un signo de tanto por ciento ( %), que trabaja sobre enteros y devuelve el resto cuando un numero se divide entre otro.

expresión booleana: Una expresión que es cierta o falsa.

operador de comparación: Uno de los operadores que comparan dos valores: ==, !=, >, = y <=.

operador lógico: Uno de los operadores que combinan expresiones booleanas: and, or y not.

sentencia condicional: Sentencia que controla el flujo de ejecución de un programa dependiendo de cierta condición.

condición: La expresión booleana de una sentencia condicional que determina que rama se ejecutara.

sentencia compuesta: Estructura de Python que esta formado por una cabecera y un cuerpo. La cabecera termina en dos puntos (:). El cuerpo tiene una sangría con respecto a la cabecera.

bloque: Grupo sentencias consecutivas con el mismo sangrado.

cuerpo: En una sentencia compuesta, el bloque de sentencias que sigue a la cabecera de la sentencia.

anidamiento: Una estructura de programa dentro de otra; por ejemplo, una sentencia condicional dentro de una o ambas ramas de otra sentencia condicional.

recursividad: El proceso de volver a llamar a la función que se esta ejecutando en ese momento.

caso base: En una función recursiva, la rama de una sentencia condicional que no ocasiona una llamada recursiva.

recursividad infinita: Función que se llama a sí misma recursivamente sin alcanzar nunca el caso base. A la larga una recursión infinita provocara un error en tiempo de ejecución.

indicador: indicador visual que invita al usuario a introducir datos.

Funciones productivas

5.1. Valores de retorno

Algunas de las funciones internas que hemos usado, como las funciones math o funciones matemáticas, han producido resultados. Llamar a la función genera un nuevo valor, que normalmente asignamos a una variable pasa usar como parte de una expresión.

   1: import math

   2: e = math.exp(1.0)

   3: altura = radio * math.sin(angulo)

Pero hasta ahora, ninguna de las funciones que hemos escrito ha devuelto un valor.

En este capítulo escribiremos funciones que devuelvan valores, que llamaremos funciones productivas, a falta de un nombre mejor. El primer ejemplo es área, que devuelve el area de un c³rculo con un radio dado:

   1: import math

   2: def area(radio):

   3: temporal = math.pi * radio**2

   4: return 

   5: temporal

Ya hemos visto antes la sentencia return, pero en una funcion productiva la sentencia return incluye un valor de retorno. Esta sentencia quiere decir “retorna inmediatamente de la funcion y usa la siguiente expresion como valor de retorno”. La expresion dada puede ser arbitrariamente complicada; así pues, podríamos haber escrito esta funcion mas concisamente:

   1: def area(radio):

   2:     return math.pi * radio**2

Por otra parte, las variables temporales como temporal suelen hacer mas fácil el depurado.

A veces es útil disponer de varias sentencias de retorno, una en cada rama de una condición:

   1: def valorAbsoluto(x):

   2:     if x < 0:

   3:         return -x

   4:     else:

   5:         return x

Puesto que estas sentencias return estan en una condicion alternativa, solo se ejecutara una de ellas. En cuanto se ejecuta una de ellas, la funcion termina sin ejecutar ninguna de las sentencias siguientes.

El codigo que aparece despues de una sentencia return o en cualquier otro lugar donde el flujo de ejecucion no pueda llegar, recibe el nombre de codigo muerto.

En una funcion productiva es una buena idea asegurarse de que cualquier posible recorrido del programa alcanza una sentencia return. Por ejemplo:

   1: def valorAbsoluto(x):

   2:     if x < 0:

   3:         return -x

   4:     elif x > 0:

   5:     return x

Este programa no es correcto porque si resulta que x vale 0, entonces no se cumple ninguna de ambas condiciones y la funcion termina sin alcanzar la sentencia return. En este caso, el valor de retorno es un valor especial llamado None:

   1: >>> print valorAbsoluto(0)

   2: None

Como actividad, escriba una funcion comparar que devuelva 1 si x>y , 0 si x == y , y -1 si x <y .

Llegados a este punto, tendría que poder mirar a funciones Python completas y adivinar que hacen. También, si ha hecho los ejercicios, habrá escrito algunas funcioncillas. Tal como vaya escribiendo funciones mayores puede empezar a experimentar mas dificultades, especialmente con los errores en tiempo de ejecución y los semánticos.

Para lidiar con programas de complejidad creciente, vamos a sugerirle una técnica que llamaremos desarrollo incremental. El objetivo del desarrollo incremental es sustituir largas sesiones de depuración por la adición y prueba de pequeñas porciones de código en cada vez.

Por ejemplo, supongamos que desea encontrar la distancia entre dos puntos, dados por las coordenadas (x1; y1) y (x2; y2). Por el teorema de Pitágoras, podemos escribir la distancia es:

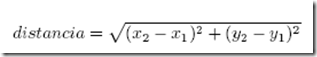
El primer paso es considerar que aspecto tendría una función distancia en Python. En otras palabras, ¿cuales son las entradas (parámetros) y cual es la salida (valor de retorno)?

En este caso, los dos puntos son los parámetros, que podemos representar usando cuatro parámetros. El valor de retorno es la distancia, que es un valor en coma flotante.

Ya podemos escribir un bosquejo de la función:

   1: def distancia(x1, y1, x2, y2):

   2: return 0.0

Obviamente, la funcion no calcula distancias; siempre devuelve cero. Pero es sintacticamente correcta y se ejecutara, lo que signi¯ca que podemos probarla antes de complicarla mas.

Para comprobar la nueva funcion, tenemos que llamarla con valores de ejemplo:

   1: >>> def distancia(x1, y1, x2, y2):

   2: ... return 

   3: 0.0

   4: ...

   5: >>> distancia(1, 2, 4, 6)

   6: 0.0

   7: >>>

Elegimos estos valores de tal forma que la distancia horizontal sea igual a 3 y la distancia vertical sea igual a 4; de esa manera el resultado es 5 (la hipotenusa del triangulo 3-4-5). Cuando se comprueba una funcion, es util saber la respuesta
correcta.

Hasta el momento, hemos comprobado que la funcion es sintacticamente correcta, así que podemos empezar a añadir líneas de codigo. Despues de cada cambio incremental, comprobamos de nuevo la funcion. Si en un momento dado aparece un error, sabremos donde esta exactamente: en la ultima l³nea que hayamos añadido.

El siguiente paso en el calculo es encontrar las diferencias entre x2¡x1 y y2¡y1.

Almacenaremos dichos valores en variables temporales llamadas dx y dy y las imprimiremos.

   1: def distancia(x1, y1, x2, y2):

   2:     dx = x2 - x1

   3:     dy = y2 - y1

   4:     print "dx es", 

   5:     dx

   6:     print "dy es", dy

   7:     return 0.0

Si la funcion funciona, valga la redundancia, las salidas deberían ser 3 y 4. Si es así, sabemos que la funcion recibe correctamente los parametros y realiza correctamente el primer calculo. Si no, solo hay unas pocas líneas que revisar.

Ahora calculamos la suma de los cuadarados de dx y dy:

   1: def distancia(x1, y1, x2, y2):

   2:     dx = x2 - x1

   3:     dy = y2 - y1

   4:     dalcuadrado = 

   5:     dx**2 + dy**2

   6:     print "dalcuadrado es: ", dalcuadrado

   7:     return 0.0

Fíjese en que hemos eliminado las sentencias print que escribimos en el paso anterior. Este codigo se llama andamiaje porque es util para construir el programa pero no es parte del producto final.

De nuevo querremos ejecutar el programa en este estado y comprobar la salida (que debería dar 25).

Por ultimo, si hemos importado el modulo math, podemos usar la funcion sqrt para calcular y devolver el resultado:

   1: def distancia(x1, y1, x2, y2):

   2: dx = x2 - x1

   3: dy = y2 - y1

   4: dalcuadrado = 

   5: dx**2 + dy**2

   6: resultado = math.sqrt(dalcuadrado)

   7: return resultado

Si esto funciona correctamente, ha terminado. Si no, podría ser que quisiera usted imprimir el valor de resultado antes de la sentencia return.

Al principio, deber³a a~nadir solamente una o dos l³neas de codigo cada vez.

Conforme vaya ganando experiencia, puede que se encuentre escribiendo y depurando trozos mayores. Sin embargo, el proceso de desarrollo incremental puede

ahorrarle mucho tiempo de depurado.
Los aspectos fundamentales del proceso son:

1. Comience con un programa que funcione y hagale pequeños cambios in-
crementales. Si hay un error, sabra exactamente donde esta.
2. Use variables temporales para mantener valores intermedios, de tal manera
que pueda mostrarlos por pantalla y comprobarlos.
3. Una vez que el programa este funcionando, tal vez prefiera eliminar parte
del andamiaje o aglutinar multiples sentencias en expresiones compuestas,
pero solo si eso no hace que el programa sea difícil de leer.
Como actividad, utilice el desarrollo incremental para escribir una
funcion de nombre hipotenusa que devuelva la longitud de la hipo-
tenusa de un triangulo rectangulo, dando como parametros los dos
catetos. Registre cada estado del desarrollo incremental segun vaya
avanzando.