herencia: La capacidad de definir una nueva clase que es una versión modificada de una clase previamente definida.
clase padre: Aquella clase de la cual la clase hija hereda.
clase hija: Una nueva clase creada heredando de una clase existente también se la llama “subclase”.
Hemos visto ejemplos de atributos que hacen referencia a otros objetos, a los que llamamos referencias incrustadas (véase la Sección 12.8). Una estructura de datos común, la lista enlazada, saca partido de esta característica.
Las listas enlazadas se componen de nodos, donde cada nodo contiene una referencia al próximo nodo de la lista. Además, cada nodo contiene una unidad de datos llamada carga.
Podemos considerar una lista enlazada como una estructura de datos recursiva porque tiene una definición recursiva.
Una lista enlazada puede ser:
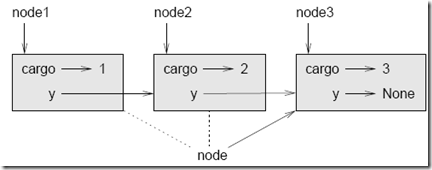
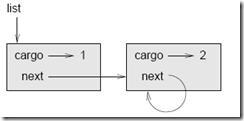
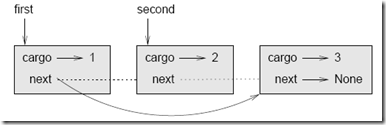
Como es habitual cuando se escribe una clase, comenzaremos con los métodos de inicialización y __str__ , para poder comprobar el mecanismo básico de crear y mostrar el nuevo tipo:
1: class Nodo:
2: def __init__(self, carga=None, siguiente=None):
3: self.carga = carga
4: self.siguiente = siguiente
5: def __str__(self):
6: return str(self.carga)
Como es habitual, los parámetros para el metodo de inicialización son opcionales. Por defecto, la carga y el enlace, siguiente, se ponen a None.
La representación alfanumérica de un nodo es únicamente la de la carga. Como se puede pasar cualquier valor a la función str, podemos guardar cualquier valor en una lista.
Para comprobar la implementación en este punto, podemos crear un Nodo e imprimirlo:
1: >>> nodo = Nodo("prueba")
2: >>> print nodo
3: prueba
Para hacerlo más interesante, necesitaremos una lista que contenga más de un nodo:
1: >>> nodo1 = Nodo(1)
2: >>> nodo2 = Nodo(2)
3: >>> nodo3 = Nodo(3)
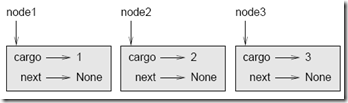
Este código crea tres nodos, pero aun no tenemos una lista porque los nodos todavía no están enlazados. El diagrama de estados tiene el siguiente aspecto:
Para enlazar los nodos, debemos hacer que el primer nodo haga referencia al segundo, y que este haga referencia al tercero:
1: >>> nodo1.siguiente = nodo2
2: >>> nodo2.siguiente = nodo3
La referencia del tercer nodo será None, que indica que es el final de la lista.
Ahora el diagrama de estados tendrá el siguiente aspecto:
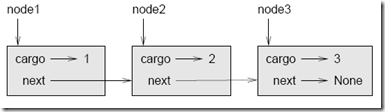
Ahora ya sabe como crear nodos y enlazarlos en listas. Lo que podría estar menos claro es por que.
Las listas son útiles porque aportan un modo de ensamblar múltiples objetos dentro de una única entidad, a veces llamada colección. En el ejemplo, el primer nodo de la lista sirve como referencia a la lista completa.
Para pasar la lista como parámetro, solo tenemos que hacer referencia al primer nodo. Por ejemplo, la función imprimeLista toma como argumento un nodo simple. Empezando con la cabeza de la lista, imprime cada nodo hasta que llega al final.
1: def imprimeLista(nodo):
2: while nodo:
3: print nodo,
4: nodo = nodo.siguiente
5: print
1: >>> imprimeLista(nodo1)
2: 1 2 3
Dentro de imprimeLista tenemos una referencia al primer nodo de la lista, pero no hay una variable que haga referencia a los otros nodos. Tendremos que usar el valor de siguiente de cada nodo para acceder al siguiente nodo.
Para recorrer una lista enlazada es habitual usar la variable de un bucle como nodo para hacer referencia sucesivamente a cada uno de los nodos.
Este diagrama muestra el valor de lista y los valores que va tomando nodo:
Por convenio, las listas suelen imprimirse entre corchetes con comas entre los elementos, como [1, 2, 3]. Como ejercicio, modifique imprimeLista para que genere una salida con este formato.
Es natural expresar muchas operaciones con listas por medio de métodos recursivos. El siguiente ejemplo es un algoritmo recursivo para imprimir una lista hacia atrás:
Por supuesto, el paso 2, la llamada recursiva, supone que tenemos una manera de imprimir una lista del revés. Pero si suponemos que la llamada recursiva funciona |el acto de fe| entonces podemos estar convencidos de que este
algoritmo funciona.
Todo lo que necesitamos es un caso básico y una forma de demostrar que para cualquier lista podemos obtener el caso básico. Dada la definición recursiva de una lista, un caso básico natural es la lista vacía, representada por None:
1: def imprimeAlReves(lista):
2: if lista == None: return
3: cabeza = lista
4: cola = lista.siguiente
5: imprimeAlReves(cola)
6: print cabeza,
La primera línea maneja el caso inicial no haciendo nada. Las dos siguientes líneas dividen la lista en cabeza y cola. Las dos ultimas líneas imprimen la lista. La coma que hay al final de la ultima l³nea evita que Python salte de línea después de imprimir un nodo.
Llamamos este metodo tal como antes invocamos a imprimeLista:
1: >>> imprimeAlReves(nodo1)
2: 3 2 1
El resultado es una lista invertida.
Es posible que se pregunte por que imprimeLista e imprimeAlReves son funciones y no métodos de la clase Nodo. La razón es que queremos usar None para representar la lista vacía y no es legal llamar un metodo sobre None. Esta limitación resulta algo incomoda a la hora de escribir código para manipular listas con un estilo orientado a objetos puro.
¿Podemos demostrar que imprimeAlReves siempre acabara? En otras palabras,
¿siempre alcanzaremos el caso básico? De hecho, la respuesta es no. Algunas listas harán que el metodo no funcione.
No hay nada que impida a un nodo hacer referencia a un nodo anterior de la lista, incluido el mismo. Por ejemplo, esta figura muestra una lista con dos nodos, uno de los cuales apunta a si mismo:
Si llamamos a imprimeLista sobre esta lista, entrara en un bucle infinito. Si llamamos a imprimeAlReves, lo hará de forma infinitamente recursiva. Este tipo de comportamiento da lugar a que sea muy difícil trabajar con listas infinitas.
Sin embargo, en ocasiones resultan útiles. Por ejemplo, podríamos representar un numero como una lista de dígitos y usar una lista infinita para representar una fracción repetida.
A pesar de todo, es un problema que no podamos probar que imprimeLista e imprimeAlReves puedan terminar correctamente. Lo mejor que podemos hacer es armar que si la lista no contiene bucles, estos métodos podrán terminar”.
Este tipo de afirmaciones se conocen como condiciones previas. Imponen una restricción sobre uno de los parámetros y describen el comportamiento del metodo si la restricción se satisface. Veremos mas ejemplos mas adelante.
Una parte de imprimeAlReves podría habernos sorprendido:
1: cabeza = lista
2: cola = lista.siguiente
Después de la primera asignación, la cabeza y la cola tienen el mismo tipo y el mismo valor. Así que, ¿para que hemos creado un nueva variable?
La razón es que las dos variables desempeñan papeles diferentes. Pensamos en la cabeza como una referencia al primer nodo de la lista. Estos “papeles” no forman parte del programa, sino que están en la mente del programador.
En general no podemos decir con solo mirar un programa que papel desempeñara un variable. Esta ambigÄuedad puede ser útil, pero también puede dificultar la lectura del programa. A menudo usaremos nombres para las variables como nodo y lista para explicar como queremos usar una variable y a veces creamos variables adicionales para eliminar ambigüedades.
Podríamos haber escrito imprimeAlReves sin cabeza ni cola, que lo haría mas conciso, pero posiblemente menos claro:
1: def imprimeAlReves(lista) :
2: if lista == None : return
3: imprimeAlReves(lista.siguiente)
4: print lista,
Mirando esas dos llamadas, hemos de recordar que imprimeAlReves trata sus argumentos como una colección y print los trata como a un solo objeto.
El teorema fundamental de la ambigüedad indica que la ambigüedad que es inherente a una referencia a un nodo:
Una variable que hace apunta a nodo puede tratar a este nodo como un objeto o como el primero de una lista de nodos.
Hay dos formas de modificar una lista enlazada. Obviamente, podemos cambiar la carga de uno de los nodos, pero las operaciones mas interesantes son las que añaden, quitan o reordenan los nodos.
Como ejemplo, escribamos un metodo que quite el segundo nodo de la lista y devuelva una referencia al nodo quitado:
1: def eliminaSegundo(lista):
2: if lista == None: return
3: primero = lista
4: segundo = lista.siguiente
5: # hacer que el primer noda apunte al tercero
6: primero.siguiente = segundo.siguiente
7: # separar el segundo nodo del resto de la lista
8: segundo.siguiente = None
9: return segundo
De nuevo, estamos usando variables temporales para hacer mas legible el código.
Así es como usamos este método:
1: >>> imprimeLista(nodo1)
2: 1 2 3
3: >>> eliminado = elimnaSegundo(nodo1)
4: >>> imprimeLista(eliminado)
5: 2
6: >>> imprimeLista(nodo1)
7: 1 3
¿Que ocurriría si llamáramos a este metodo y pasáramos una lista de un único elemento (un singleton)?
¿Que sucederá si pasáramos una lista vacía como argumento?
¿Hay una condición previa para este metodo? Si es así, será algo razonable establecer un metodo para manejar una violación de la condición previa.
Creado con WordPress & Tema de Anders Norén