Categoría: ser mejor programador Página 3 de 5

en clonar listas, Cursos de programación, Cursos de programación Python, Lista, Pensar como programador, Pyhon, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

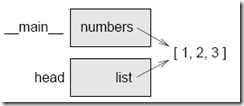
Si queremos modificar una lista y mantener una copia del original, necesitaremos ser capaces de hacer una copia de la lista en sí, no solo de su referencia. Este proceso a veces se denomina clonado, para evitar la ambigüedad de la palabra ”copia”.

La forma mas fácil de clonar una lista es por medio del operador de porción:

>>> a = [1, 2, 3]
>>> b = []
>>> b[:] = a[:]
>>> print b
[1, 2, 3]

La extracción de una porción de a crea una nueva lista. En este caso, la porción consta de la lista completa.

Ahora tenemos libertad de hacer cambios en b sin preocuparnos de a:

>>> b[0] = 5
>>> print a
[1, 2, 3]

Como ejercicio, dibuje un diagrama de estado de a y b antes y después del cambio.

8.13. Listas como parámetros

en Cursos de programación, Cursos de programación Python, Listas como parámetros, Pensar como programador, Pyhon, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

Cuando se pasa una lista como argumento, en realidad se pasa una referencia a ella, no una copia de la lista. Por ejemplo, la función cabeza toma una lista como parámetro y devuelve el primer elemento.

   1: def cabeza(lista):
   2:     return lista[0]

Así es como se usa.

>>> numeros = [1,2,3]
>>> cabeza(numeros)
1

El parámetro lista y la variable números son alias de un mismo objeto. El diagrama de estado es así:

Como el objeto lista esta compartido por dos marcos, lo dibujamos entre ambos.

Si la función modifica una lista pasada como parámetro, el que hizo la llamada vera el cambio. borra cabeza elimina el primer elemento de una lista.

   1: def borra_cabeza(lista):
   2:     del lista[0]

Aquí vemos el uso de borra cabeza:

Si una función devuelve una lista, de

>>> numeros = [1,2,3]
>>> borra_cabeza(numeros)
>>> print numeros
[2, 3]

vuelve una referencia a la lista. Por ejemplo, cola devuelve una lista que contiene todos los elementos de una lista dada, excepto el primero.

   1: def cola(lista):
   2: return lista[1:]

Aquí vemos como se usa cola:

>>> numeros = [1,2,3]
>>> resto = cola(numeros)
>>> print resto
>>> [2, 3]

Como el valor de retorno se creo con una porción, es una lista. La creación de rest, así como cualquier cambio posterior en rest, no afectara a numbers.

8.15. Matrices

en Cursos de programación, Cursos de programación Python, matrices, Pensar como programador, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

Es común usar listas anidadas para representar matrices. Por ejemplo, la matriz:

1 2 3
7 8 9
4 5 6

puede ser representada como:

   1: >>> matriz = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]

matriz es una lista con tres elementos, siendo cada elemento una fila de la matriz. Podemos elegir una fila entera de la matriz de la forma normal:

   1: >>> matriz[1]
   2: [4, 5, 6]

O tomar solo un elemento de la matriz usando la forma de doble índice:

   1: >>> matriz[1][1]
   2: 5

El primer índice escoge la fila y el segundo la columna. Aunque esta manera de representar matrices es común, no es la única posibilidad. Una pequeña variación consiste en usar una lista de columnas en lugar de filas. Mas adelante veremos una alternativa mas radical usando un diccionario.

8.16. Cadenas y listas

en cadenas, Cursos de programación, Cursos de programación Python, Lista, Pensar como programador, Pyhon, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

Dos de las funciones mas útiles del modulo string tienen que ver con listas de cadenas. La función split divide una cadena en una lista de palabras. Por defecto, cualquier numero de caracteres de espacio en blanco se considera un límite de palabra:

>>> import string
>>> cancion = "La lluvia en Sevilla..."
>>> string.split(cancion)
['La', 'lluvia', 'en', 'Sevilla...']

Se puede usar un argumento opcional llamado delimitador para especificar que caracteres se usaran como límites de palabra. El siguiente ejemplo usa la cadena ll como delimitador:

   1: >>> string.split(cancion, 'll')
   2: ['La ', 'uvia en Sevi', 'a...']

Observe que el delimitador no aparece en la lista.

La función join es la inversa de split. Toma una lista de cadenas y concatena

los elementos con un espacio entre cada par:

>>> lista = ['La', 'lluvia', 'en', 'Sevilla...']
>>> string.join(lista)
'La lluvia en Sevilla...'

Como split, join acepta un delimitador opcional que se inserta entre los elementos. El delimitador por defecto es el espacio.

   1: >>> string.join(lista, '_')
   2: 'La_lluvia_en_Sevilla...'

A modo de ejercicio, describa la relación que hay entre
string.join(string.split(cancion)) y canción. ¿Esla misma para todas las cadenas?
¿Cuando sería diferente?

8.17. Glosario

en Cursos de programación, Cursos de programación Python, indice, Lista, Pensar como programador, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

lista: Una colección de objetos con nombre, en la que cada objeto es identificado por un índice.

índice: Una variable o valor enteros que se usan para indicar un elemento de una lista.

elemento: Uno de los valores de una lista (u otra secuencia). El operador corchete selecciona elementos de una lista.

secuencia: Cualquier tipo de datos que consista en un conjunto ordenado de elementos, con cada elemento identificado por un índice.

lista anidada: Una lista que es elemento de otra lista.

recorrido de lista: Acceso secuencial a cada elemento de una lista.

objeto: Una cosa a la que se puede referir una variable.

alias: Múltiples variables que contienen referencias al mismo objeto.

clonar: Crear un objeto nuevo que tiene el mismo valor que un objeto ya existente. Copiar una referencia a un objeto crea un alias, pero no clona el objeto.

delimitador: Un carácter o cadena utilizado para indicar donde debe cortarse una cadena.

Crear un nuevo tipo de datos en Python

en Cursos de programación, Cursos de programación Python, Pensar como programador, Pyhon, ser mejor programador, Tecnicas para programar mejor

Los lenguajes de programación orientados a objetos permiten a los programadores crear nuevos tipos de datos que se comporten de manera muy parecida a los tipos de datos nativos. Exploraremos esta posibilidad construyendo una clase Fracción que funcione de manera muy similar a los tipos numéricos nativos, enteros, enteros largos y flotantes.

Las fracciones, también conocidas como números racionales, son valores que pueden expresarse como la proporción entre dos números enteros, tal como 5=6.

Al numero superior se se le llama numerador y al inferior se se le llama denominador.

Comenzamos definiendo la clase Fracción con un método de inicialización que nos surta de un numerador y un denominador enteros:

   1: class Fracción:

   2:     def __init__(self, numerador, denominador=1):

   3:         self.numerador = numerador

   4:         self.denominador = denominador

El denominador es opcional. Una Fracción con un solo parámetro representa un numero entero. Si el numerador es n, construimos la fracción n=1.

El siguiente paso es escribir un método str para que imprima las fracciones de forma que tenga sentido. La forma natural de hacerlo es numerador/denominador”:

   1: class Fracción:

   2:     ...

   3:     def __str__(self):

   4:     return "%d/%d" % (self.numerador, self.denominador)

Para probar lo que tenemos hasta ahora, lo ponemos en un ¯chero llamado Fracción.py y lo importamos desde el interprete de Python. Entonces creamos un objeto fracción y lo imprimimos.

>;>> from Fracción import fracción

>;>> mortadela = Fracción(5,6)

>;>> print "La fracción es", mortadela

La fracción es 5/6

Como siempre, la función print invoca implícitamente al método str .

B.1. Multiplicación de fracciones Python

en Cursos de programación, Cursos de programación Python, Pensar como programador, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

Nos gustaría poder aplicar las operaciones normales de suma, resta, multiplicación y división a las fracciones. Para ello, podemos sobrecargar los operadores matemáticos para los objetos de clase Fracción.

Comenzaremos con la multiplicación porque es la mas fácil de implementar.

Para multiplicar dos fracciones, creamos una nueva fracción cuyo numerador es el producto de los numeradores de los operandos y cuyo denominador es el producto de los denominadores de los operandos. __mul__ es el nombre que Python utiliza para el método que sobrecarga al operador *:

class Fracción:

...

    def __mul__(self, otro):

        return Fracción(self.numerador*otro.numerador,

            self.denominador*otro.denominador)

Podemos probar este método calculando el producto de dos fracciones:

>;>> print Fracción(5,6) * Fracción(3,4)

15/24

Funciona, pero podemos hacerlo mejor! Podemos ampliar el método para manejar la multiplicación por un entero.

Usamos la función type para ver si otro es un entero y convertirlo en una fracción en tal caso.

class Fracción:

...

    def __mul__(self, otro):

        if type(otro) == type(5):

        otro = Fracción(otro)

        return Fracción(self.numerador * otro.numerador,

        self.denominador * otro.denominador)

Ahora funciona la multiplicación para fracciones y enteros, pero solo si la fracción es el operando de la izquierda.

>;>> print Fracción(5,6) * 4

20/6

>;>> print 4 * Fracción(5,6)

TypeError: __mul__ nor __rmul__ defined for these operands

Para evaluar un operador binario como la multiplicación, Python comprueba primero el operando de la izquierda para ver si proporciona un método __mul__ que soporte el tipo del segundo operando. En este caso, el operador nativo de multiplicación del entero no soporta fracciones.
Después, Python comprueba el segundo operando para ver si provee un método __rmul__ que soporte el tipo del primer operando. En este caso, no hemos provisto el método rmul , por lo que falla.

Por otra parte, hay una forma sencilla de obtener __rmul __:

class Fracción:

...

__rmul__ = __mul__

Esta asignación hace que el método rmul sea el mismo que __mul__ . Si ahora evaluamos 4 * Fracción(5,6), Python llamaría al método __rmul__ del objeto Fracción y le pasara 4 como parámetro:

>;>> print 4 * Fracción(5,6)

20/6

Dado que rmul es lo mismo que __mul__ , y __mul__ puede manejar un parámetro entero, ya esta hecho.

B.2. Suma de fracciones Python

en Cursos de programación, Cursos de programación Python, Pensar como programador, Pyhon, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

La suma es mas complicada que la multiplicación, pero aun es llevadera. La suma de a=b y c=d es la fracción (a*d+c*b)/b*d.
Usando como modelo el código de la multiplicación, podemos escribir __add__ y __radd__:

class Fracción:

...

    def __add__(self, otro):

        if type(otro) == type(5):

        otro = Fracción(otro)

    return Fracción(self.numerador * otro.denominador +

    self.denominador * otro.numerador,

    self.denominador * otro.denominador)

    __radd__ = __add__

Podemos probar estos métodos con Fracciones y enteros.

>;>> print Fracción(5,6) + Fracción(5,6)

60/36

>;>> print Fracción(5,6) + 3

23/6

>;>> print 2 + Fracción(5,6)

17/6

Los dos primeros ejemplos llaman a __add__ ; el ultimo llama a __radd__ .

B.4. Comparar fracciones Python

en Cursos de programación, Cursos de programación Python, Pensar como programador, Pyhon, ser mejor programador, técnica para programar mejor, Tecnicas para programar mejor

Supongamos que tenemos dos objetos Fracción, a y b, y evaluamos a == b. La implementación por defecto de == comprueba la igualdad super¯cial, por lo que solo devuelve true si a y b son el mismo objeto.

Queremos mas bien devolver verdadero si a y b tienen el mismo valor |eso es,igualdad en profundidad.

Hemos de enseñar a las fracciones como compararse entre si. Como vimos en la Sección 15.4, podemos sobrecargar todos los operadores de comparación de una vez proporcionando un método cmp .

Por convenio, el método cmp devuelve un numero negativo si self es menor que otro, zero si son lo mismo, y un numero positivo si self es mayor que otro.

La forma mas simple de comparar dos fracciones es la multiplicación cruzada.

Si a=b > c=d, entonces ad > bc. Con esto en mente, aquí esta el código para cmp :

   1: class Fraccion:

   2: ...

   3:     def __cmp__(self, otro):

   4:         dif = (self.numerador * otro.denominador -

   5:             otro.numerador * self.denominador)

   6:         return dif

Si self es mayor que otro, entonces dif sera positivo. Si otro es mayor, entonces dif sera negativo. Si son iguales, dif es cero.

B.5. Forzando la máquina